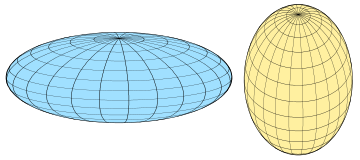
椭圆围绕一个垂直轴旋转而成的类球面
扁球面
长球面
类球面 是一种二次曲面 。二维的椭圆 有两个主轴,称为长轴 与短轴 。在三维空间里,将一个椭圆绕着其任何一主轴旋转,则可得到一个类球面。
假若,这旋转主轴是长轴,则这个类球面为长球面。例如,英式足球 里所用的橄榄球 是长球形状。
假若,这旋转主轴是短轴,则这个类球面为扁球面。例如,地球 在北极与南极稍微有点扁平,在赤道又有点凸涨。所以,地球是扁球形状。
假若,生成的椭圆是圆圈 ,则这个类球面为完全对称的圆球面 。 方程式
对类球面半轴的赋值。如果
c < a 则为扁球面(左图)而如果
c > a 则为长球面(右图)。
用另外一种方法来描述,类球面是一种椭球面 。采用直角坐标
(
x
,
y
,
z
)
{\displaystyle (x,\ y,\ z)\,\!}
x
2
a
2
+
y
2
b
2
+
z
2
c
2
=
1
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1}
其中,
a
{\displaystyle a\,\!}
b
{\displaystyle b\,\!}
赤道半径 ,
c
{\displaystyle c\,\!}
极半径 ,这三个正值实数的半径决定了椭球面的形状。 以z-轴为旋转轴的类球面
a
=
b
{\displaystyle a=b\,}
x
2
+
y
2
a
2
+
z
2
c
2
=
1
{\displaystyle {\frac {x^{2}+y^{2}}{a^{2}}}+{\frac {z^{2}}{c^{2}}}=1}
a
=
c
{\displaystyle a=c\,\!}
假若,类球面的赤道半径小于极半径,则这是类球面是长球面:
a
<
c
{\displaystyle a<c\,\!}
假若,类球面的赤道半径大于极半径,则这是类球面是扁球面:
a
>
c
{\displaystyle a>c\,\!}
性质
面积 扁球面c < a 表面积 为:
S
o
b
l
a
t
e
=
2
π
a
2
(
1
+
1
−
e
2
e
artanh
e
)
=
2
π
a
2
+
π
c
2
e
ln
(
1
+
e
1
−
e
)
{\displaystyle S_{\rm {oblate}}=2\pi a^{2}\left(1+{\frac {1-e^{2}}{e}}{\text{artanh}}\,e\right)=2\pi a^{2}+\pi {\frac {c^{2}}{e}}\ln \left({\frac {1+e}{1-e}}\right)\quad }
e
2
=
1
−
c
2
a
2
{\displaystyle \,e^{2}=1-{\frac {c^{2}}{a^{2}}}}
扁球面是半长轴为a c z e 离心率 [1]
长球面c > a
S
p
r
o
l
a
t
e
=
2
π
a
2
(
1
+
c
a
e
arcsin
e
)
{\displaystyle S_{\rm {prolate}}=2\pi a^{2}\left(1+{\frac {c}{ae}}\arcsin \,e\right)\qquad }
e
2
=
1
−
a
2
c
2
{\displaystyle \,e^{2}=1-{\frac {a^{2}}{c^{2}}}}
长球面是半长轴为c a z e 离心率 [2]
体积 类球的体积是
4
3
π
a
2
c
{\displaystyle {\frac {4}{3}}\pi a^{2}c\,\!}
曲率 假若,一个类球面被参数化为
σ
(
β
,
λ
)
=
(
a
cos
β
cos
λ
,
a
cos
β
sin
λ
,
b
sin
β
)
{\displaystyle {\boldsymbol {\sigma }}(\beta ,\ \lambda )=(a\cos \beta \cos \lambda ,\ a\cos \beta \sin \lambda ,\ b\sin \beta )\,\!}
其中,
β
{\displaystyle \beta \,\!}
参数纬度 (parametric latitude ),
−
π
2
<
β
<
π
2
{\displaystyle -{\frac {\pi }{2}}<\beta <{\frac {\pi }{2}}\,\!}
λ
{\displaystyle \lambda \,\!}
经度 ,
−
π
<
λ
<
+
π
{\displaystyle -\pi <\lambda <+\pi \,\!}
那么,类球面的高斯曲率 (Gaussian curvature )是
K
(
β
,
λ
)
=
b
2
(
a
2
+
(
b
2
−
a
2
)
cos
2
β
)
2
{\displaystyle K(\beta ,\lambda )={b^{2} \over (a^{2}+(b^{2}-a^{2})\cos ^{2}\beta )^{2}}\,\!}
类球面的平均曲率 (mean curvature )是
H
(
β
,
λ
)
=
b
(
2
a
2
+
(
b
2
−
a
2
)
cos
2
β
)
2
a
(
a
2
+
(
b
2
−
a
2
)
cos
2
β
)
3
/
2
{\displaystyle H(\beta ,\lambda )={b(2a^{2}+(b^{2}-a^{2})\cos ^{2}\beta ) \over 2a(a^{2}+(b^{2}-a^{2})\cos ^{2}\beta )^{3/2}}\,\!}
对于类球面,这两种曲率永远是正值的。所以,类球面的每一点都是椭圆的。
参阅 引用
^ A derivation of this result may be found at Weisstein, Eric W. (编). Oblate Spheroid . at MathWorld Wolfram Research, Inc. [24 June 2014] . (原始内容存档 于2018-01-24) (英语) .
^ A derivation of this result may be found at Weisstein, Eric W. (编). Prolate Spheroid . at MathWorld Wolfram Research, Inc. [24 June 2014] . (原始内容存档 于2019-10-21) (英语) .