坐标曲面

一个三维坐标系的坐标曲面，是这坐标系中，一个坐标的等值曲面；称为这个坐标的坐标曲面。一个三维坐标系的坐标曲线，是这坐标系中，两个不同坐标曲面的交集。所以，这坐标曲线有两个坐标是常数；称这坐标曲线为另外一个坐标的坐标曲线。

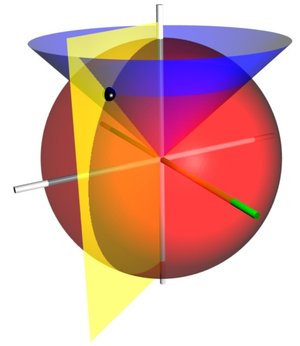
球坐标 ${\displaystyle (r,\ \theta ,\ \phi )\,\!}$ 的坐标曲面。红色的圆球面是 ${\displaystyle r=2\,\!}$ 等值面。蓝色的圆锥面是 ${\displaystyle \theta =45^{\circ }\,\!}$ 等值面。黄色的半平面是 ${\displaystyle \phi =-60^{\circ }\,\!}$ 等值面。 z-轴是垂直的。 x-轴是绿色的。三个坐标曲面相交于点 P （以黑球表示）。

举例而言，球坐标系 ${\displaystyle (r,\ \theta ,\ \phi )\,\!}$ 的径向距 ${\displaystyle r\,\!}$-坐标曲面是个圆球面：

${\displaystyle r=R\,\!}$ ；

其中，${\displaystyle R\,\!}$ 是常数 。

用直角坐标 ${\displaystyle (x,\ y,\ z)\,\!}$ 来表示：

${\displaystyle x^{2}+y^{2}+z^{2}=R^{2}\,\!}$ 。

相似地，天顶角 ${\displaystyle \theta \,\!}$-坐标曲面是圆锥面，方位角 ${\displaystyle \phi \,\!}$-坐标曲面是半平面。

球坐标系的径向距 ${\displaystyle r\,\!}$-坐标曲线，是从原点往外方的径向射线，是 ${\displaystyle \theta \,\!}$-坐标曲面与 ${\displaystyle \phi \,\!}$-坐标曲面的交集。

坐标单位向量是垂直于坐标曲面的单位向量。坐标单位向量指向坐标曲面的等值坐标最快增值的方向。例如，球座标系的径向坐标单位向量 ${\displaystyle \mathbf {e} _{r}\,\!}$ 与径向单位向量 ${\displaystyle {\hat {\mathbf {r} }}\,\!}$ 同方向；是径向距 ${\displaystyle r\,\!}$ 最快增值的方向。

在二维坐标系里，坐标曲线也有定义：每一个坐标的坐标曲线就是另外一个坐标的等值曲线。