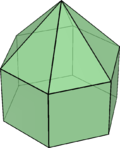
六角锥柱
在几何学中,六角锥柱是一种多面体,是锥柱体的一种,指底面为六边形的锥柱体,或是将底面全等的六角锥与六角柱叠合所形成的立体。六角锥柱具有13个面、24个边、和13个顶点,每个六角锥柱皆为一个十三面体。
 | ||
| 类别 | 棱锥柱 拟约翰逊多面体 | |
|---|---|---|
| 对偶多面体 | 六角锥柱(自身对偶) | |
| 数学表示法 | ||
| 康威表示法 | P6+Y6 | |
| 性质 | ||
| 面 | 13 | |
| 边 | 24 | |
| 顶点 | 13 | |
| 欧拉特征数 | F=13, E=24, V=13 (χ=2) | |
| 组成与布局 | ||
| 面的种类 | 6个三角形 6个正方形 1个六边形 | |
| 顶点布局 | 6(42.6) 6(32.42) | |
| 对称性 | ||
| 对称群 | C6v, [6], (*66) C6v群 | |
| 旋转对称群 | C6, [6]+, (66) | |
| 特性 | ||
| 凸、 demi-regular | ||
| 图像 | ||
| ||
底面为正六边形的六角锥柱称为正六角锥柱,既不是半正多面体,也不是约翰逊多面体。
正六角锥柱
正六角锥柱仅指底面为正六边形的六角锥柱,若考虑侧面皆为正多边形是不可能的,考虑六角锥柱的上下二部分,柱体部分侧面可以为正多边形:正方形,锥体部分则不行,如同六角锥,若每个面皆为正三角形,则整个六角锥柱将会退化为六角柱,因此不能算是半正多面体,也不是约翰逊多面体,但可以算是一种拟约翰逊多面体。
相关多面体
| 二角锥柱 | 三角锥柱 | 四角锥柱 | 五角锥柱 | 六角锥柱 | 七角锥柱 | ... | 圆锥柱 |
|---|---|---|---|---|---|---|---|
参见
- 拟约翰逊多面体
- 约翰逊多面体
- 六角锥