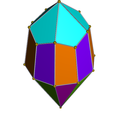
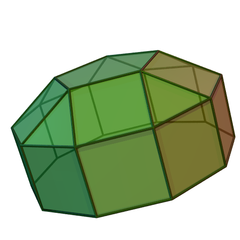
五角台塔柱
 | |||
| 类别 | 约翰逊多面体 J19 - J20 - J21 | ||
|---|---|---|---|
| 对偶多面体 | 五角半偏方面体锥柱 | ||
| 识别 | |||
| 鲍尔斯缩写 | epcu | ||
| 性质 | |||
| 面 | 22 | ||
| 边 | 45 | ||
| 顶点 | 25 | ||
| 欧拉特征数 | F=22, E=45, V=25 (χ=2) | ||
| 组成与布局 | |||
| 面的种类 | 三角形×5 正方形×15 五边形×1 十边形×1 | ||
| 顶点布局 | 10(42.10) 10(3.43) 5(3.4.5.4) | ||
| 对称性 | |||
| 对称群 | C5v | ||
| 旋转对称群 | C5v群 | ||
| 特性 | |||
| 凸多面体 | |||
| 图像 | |||
| |||
正五角台塔柱
考虑一个正五角台塔柱,当侧面皆为正多边形时则为92种约翰逊多面体(J20)中的其中一个,顾名思义,它可由一个正十角柱在一个底面上连接一底面大小相同的正五角台塔(J5)接合而成。或者也可以将同相双五角台塔柱(J38)截去一个正五角台塔而得到。这92种Johnson立体最早在1966年由Johnson Norman命名并给予描述。若边长为a此时体积和表面积可以以特定的公式表示[1]:
- 体积:
- 表面积:
对偶多面体
| Dual elongated pentagonal cupola | Net of dual |
|---|---|
参见
- 约翰逊多面体
- 正五角台塔
- 同相双五角台塔柱
参考文献
- ^ Stephen Wolfram, "Elongated pentagonal cupola (页面存档备份,存于互联网档案馆)" from Wolfram Alpha. Retrieved July 22, 2010.
- 埃里克·韦斯坦因. Elongated pentagonal cupola. MathWorld.
外部链接
- 埃里克·韦斯坦因. Johnson solid. MathWorld.