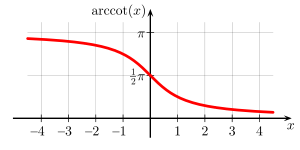
反余切 反余切函数有多种定义方式 绿色 反函数 [函数 1] 蓝色 同界角 [函数 2] 红色 复变分析 反余切实数 部[函数 3] 性质 奇偶性 非奇 非偶 定义域 实数 集 到达域
[
0
,
π
]
{\displaystyle [0,\pi ]}
[函数 2]
[
0
,
180
∘
]
{\displaystyle [0,180^{\circ }]}
[函数 2]
(
−
π
2
,
π
2
]
{\displaystyle (-{\frac {\pi }{2}},{\frac {\pi }{2}}]}
[函数 3]
(
−
90
∘
,
90
∘
]
{\displaystyle (-90^{\circ },90^{\circ }]}
[函数 3] 周期 N/A 特定值 当x=0
π
2
{\displaystyle {\frac {\pi }{2}}}
当x=+∞ 0 当x=-∞
π
{\displaystyle \pi }
[函数 2] [函数 2] [函数 3] 其他性质 渐近线
y
=
0
,
y
=
π
{\displaystyle {y=0,y=\pi }}
[函数 2]
y
=
0
,
y
=
180
∘
{\displaystyle {y=0,y=180^{\circ }}}
[函数 2]
y
=
0
{\displaystyle y=0}
[函数 3] 根 无穷大 拐点
(
0
,
π
2
)
{\displaystyle (0,{\frac {\pi }{2}})}
[函数 2]
(
0
,
90
∘
)
{\displaystyle (0,90^{\circ })}
[函数 2] 不动点 0.86033358901938...[函数 2] [注 1] ±0.86033358901938... [函数 3]
反余切 (英语:arccotangent [3]
arccot
{\displaystyle \operatorname {arccot} }
[4] [5] [6] arcctg [7] ACOT [8]
cot
−
1
{\displaystyle \cot ^{-1}}
[1] 逆余切 ,是一种反三角函数 [9] [2] 三角函数 为余切函数 ,是利用已知直角三角形 的邻边和对边这两条直角边 长度的比值 求出其夹角 大小的函数 ,但其输入值和反正切 的输入值互为倒数 ,是高等数学 中的一种基本特殊函数 。
反余切 可以视为余切 的反函数 ,但余切函数 是周期函数 且在实数 上不具有一一对应的关系,所以不存在反函数 ,但也可以视为多值函数 [函数 1] [1] 限制 余切函数的定义域 使其成为单射 和满射 也是可逆 的。
一般最常见的方式是限制余切函数 的定义域 在0 到π [10] [1] [11] 奇函数 也不是偶函数 ,而是一个单调递减 的有界函数 [12] 最大值 为
π
{\displaystyle \pi }
最小值 为0且函数连续 ,但有两条渐近线 。
另外一种定义方式是限制余切函数 的定义域 在
±
π
2
{\displaystyle \pm {\frac {\pi }{2}}}
[13] [14] 反正切 相同,此时反余切函数是奇函数 ,值域与其他相关性质皆与反正切类似,但函数并不连续。
由于余切是周期函数,而上述二种定义方式皆是取余切的一个周期,因此其定义域皆为实数 集 。但当将反余切函数扩展至复数 时,会采用后者的定义方式[4]
但由于复变分析 的定义方式会造成函数不连续[函数 3]
x
=
0
{\displaystyle x=0}
断点 ,因此应用在测量学 上时会采用取最小同界角 的方式[函数 2] [15]
反余切函数经常记为
cot
−
1
{\displaystyle \cot ^{-1}}
[1]
arccot
{\displaystyle \operatorname {arccot} }
[16] [4] [5] [6] ISO 31 -11,应将反余切函数记为
arccot
{\displaystyle \operatorname {arccot} }
cot
−
1
{\displaystyle \cot ^{-1}}
1
cot
{\displaystyle {\frac {1}{\cot }}}
1
cot
{\displaystyle {\frac {1}{\cot }}}
正切函数 。
反余切 表示余切的反函数,因此是一个多值函数[1]
将余切函数 限制在
[
0
,
π
]
{\displaystyle [0,\pi ]}
反函数 [1]
将余切函数 限制在
(
−
π
2
,
π
2
]
{\displaystyle (-{\frac {\pi }{2}},{\frac {\pi }{2}}]}
(
−
90
∘
,
90
∘
]
{\displaystyle (-90^{\circ },90^{\circ }]}
反函数 [2] 在复变分析中则是采用第二种定义延伸至复数[4]
arccot
x
=
i
2
[
ln
(
x
−
i
x
)
−
ln
(
x
+
i
x
)
]
{\displaystyle \operatorname {arccot} x={\frac {i}{2}}\left[\ln \left({\frac {x-i}{x}}\right)-\ln \left({\frac {x+i}{x}}\right)\right]}
这个动作使反余切被推广到复数 。
此外,反余切函数[函数 3] [2]
arccot
(
x
)
=
cot
−
1
(
x
)
=
{
sec
−
1
(
x
2
+
1
x
)
−
π
,
for
x
<
0
sec
−
1
(
x
2
+
1
x
)
,
for
x
>
0
=
{
−
π
2
−
tan
−
1
x
,
for
x
<
0
π
2
−
tan
−
1
x
,
for
x
>
0
∨
x
=
0
=
{
−
sin
−
1
(
1
x
2
+
1
)
,
for
x
<
0
sin
−
1
(
1
x
2
+
1
)
,
for
x
>
0
=
{
−
csc
−
1
(
x
2
+
1
)
,
for
x
<
0
csc
−
1
(
x
2
+
1
)
,
for
x
>
0
=
{
−
cos
−
1
(
x
2
+
1
x
)
−
π
,
for
x
<
0
cos
−
1
(
x
2
+
1
x
)
,
for
x
>
0
=
{
−
π
2
−
sin
−
1
(
1
x
2
+
1
)
,
for
x
<
0
π
2
−
sin
−
1
(
1
x
2
+
1
)
,
for
x
>
0
{\displaystyle {\begin{aligned}\operatorname {arccot}(x)=\cot ^{-1}(x)&={\begin{cases}\sec ^{-1}\left({\frac {\sqrt {x^{2}+1}}{x}}\right)-\pi ,&{\mbox{for }}x<0\\\sec ^{-1}\left({\frac {\sqrt {x^{2}+1}}{x}}\right),&{\mbox{for }}x>0\end{cases}}={\begin{cases}-{\frac {\pi }{2}}-\tan ^{-1}x,&{\mbox{for }}x<0\\{\frac {\pi }{2}}-\tan ^{-1}x,&{\mbox{for }}x>0\lor x=0\end{cases}}\\&={\begin{cases}-\sin ^{-1}\left({\frac {1}{\sqrt {x^{2}+1}}}\right),&{\mbox{for }}x<0\\\sin ^{-1}\left({\frac {1}{\sqrt {x^{2}+1}}}\right),&{\mbox{for }}x>0\end{cases}}={\begin{cases}-\csc ^{-1}\left({\sqrt {x^{2}+1}}\right),&{\mbox{for }}x<0\\\csc ^{-1}\left({\sqrt {x^{2}+1}}\right),&{\mbox{for }}x>0\end{cases}}\\&={\begin{cases}-\cos ^{-1}\left({\frac {\sqrt {x^{2}+1}}{x}}\right)-\pi ,&{\mbox{for }}x<0\\\cos ^{-1}\left({\frac {\sqrt {x^{2}+1}}{x}}\right),&{\mbox{for }}x>0\end{cases}}={\begin{cases}-{\frac {\pi }{2}}-\sin ^{-1}\left({\frac {1}{\sqrt {x^{2}+1}}}\right),&{\mbox{for }}x<0\\{\frac {\pi }{2}}-\sin ^{-1}\left({\frac {1}{\sqrt {x^{2}+1}}}\right),&{\mbox{for }}x>0\end{cases}}\\\end{aligned}}}
直角坐标系中 在直角坐标系 中,反余切函数可以视为已知直线 垂线斜率 的倾角,但是有可能差一个负号。
级数定义 反余切函数可以使用无穷级数 定义:
arccot
z
=
π
2
−
arctan
z
=
π
2
−
(
z
−
z
3
3
+
z
5
5
−
z
7
7
+
⋯
)
=
π
2
−
∑
n
=
0
∞
(
−
1
)
n
z
2
n
+
1
2
n
+
1
;
|
z
|
≤
1
z
≠
i
,
−
i
{\displaystyle {\begin{aligned}\operatorname {arccot} z&{}={\frac {\pi }{2}}-\arctan z\\&{}={\frac {\pi }{2}}-(z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{5}}-{\frac {z^{7}}{7}}+\cdots )\\&{}={\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{2n+1}};\qquad |z|\leq 1\qquad z\neq i,-i\end{aligned}}}
[函数 2] 对
x
>
0
{\displaystyle x>0}
[函数 3] [17]
arccot
x
=
π
2
−
∑
k
=
0
∞
(
−
1
)
k
x
2
k
+
1
2
k
+
1
=
π
2
−
x
+
x
3
3
−
x
5
5
+
x
7
7
−
⋯
{\displaystyle \operatorname {arccot} x={\frac {\pi }{2}}-\sum _{k=0}^{\infty }(-1)^{k}{\frac {x^{2k+1}}{2k+1}}={\frac {\pi }{2}}-x+{\frac {x^{3}}{3}}-{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}-\cdots }
以上等式也可以直接用来表示取最小同界角 的反余切函数[函数 2]
也可以用当
z
=
∞
{\displaystyle z=\infty }
洛朗级数 来定义,对应
|
z
|
>
1
{\displaystyle \left|z\right|>1}
arccot
z
=
∑
k
=
0
∞
(
−
1
)
k
z
−
(
2
k
+
1
)
2
k
+
1
=
1
z
−
1
3
x
3
+
1
5
x
5
−
1
7
x
7
+
1
9
x
9
−
⋯
{\displaystyle \operatorname {arccot} z=\sum _{k=0}^{\infty }(-1)^{k}{\frac {z^{-(2k+1)}}{2k+1}}={\frac {1}{z}}-{\frac {1}{3x^{3}}}+{\frac {1}{5x^{5}}}-{\frac {1}{7x^{7}}}+{\frac {1}{9x^{9}}}-\cdots }
[函数 3] 此外也有欧拉 导出的无穷级数[18]
arccot
(
z
)
=
cot
−
1
(
z
)
=
z
∑
n
=
1
∞
(
2
n
−
2
)
!
!
(
2
n
−
1
)
!
!
(
z
2
+
1
)
n
{\displaystyle \operatorname {arccot}(z)=\cot ^{-1}(z)=z\sum _{n=1}^{\infty }{\frac {(2n-2)!!}{(2n-1)!!\left(z^{2}+1\right)^{n}}}}
[函数 3] 性质
反余切函数[函数 2]
arccot
(
−
x
)
=
π
−
arccot
x
=
180
∘
−
arccot
x
{\displaystyle \operatorname {arccot}(-x)=\pi -\operatorname {arccot} x=180^{\circ }-\operatorname {arccot} x\!}
反余切函数是一个递减函数。
在复变分析中,反余切函数[函数 3]
x
{\displaystyle x}
奇函数 ,因此满足下面等式:
arccot
(
−
x
)
=
−
arccot
x
(
x
≠
0
)
{\displaystyle \operatorname {arccot}(-x)=-\operatorname {arccot} x\qquad (x\neq 0)}
反余切虽有多种定义方式,但其在
x
=
0
{\displaystyle x=0}
π
2
{\displaystyle {\frac {\pi }{2}}}
x
=
0
{\displaystyle x=0}
[函数 3]
x
=
0
{\displaystyle x=0}
反余切函数的微分导数为[注 2]
a
r
c
c
o
t
′
x
=
−
1
1
+
x
2
{\displaystyle {\rm {arccot}}'x=-{\frac {1}{1+x^{2}}}}
a
r
c
c
o
t
″
x
=
2
x
(
1
+
x
2
)
2
{\displaystyle {\rm {arccot}}''x={\frac {2x}{\left(1+x^{2}\right)^{2}\,}}}
a
r
c
c
o
t
‴
x
=
−
8
x
2
(
1
+
x
2
)
3
+
2
(
1
+
x
2
)
2
{\displaystyle {\rm {arccot}}'''x=-{\frac {8x^{2}}{\left(1+x^{2}\right)^{3}\,}}+{\frac {2}{\left(1+x^{2}\right)^{2}\,}}}
a
r
c
c
o
t
⁗
x
=
48
x
3
(
1
+
x
2
)
4
−
24
x
(
1
+
x
2
)
3
{\displaystyle {\rm {arccot}}''''x={\frac {\;48x^{3}\;}{\;\left(1+x^{2}\right)^{4}\,}}-{\frac {\;24x\;}{\;\left(1+x^{2}\right)^{3}\,}}}
⋯
{\displaystyle \cdots }
除了反正切,反余切函数同样可以表示梅钦类公式 [19]
π
4
=
4
arccot
5
−
arccot
239
{\displaystyle {\frac {\pi }{4}}=4\operatorname {arccot} {5}-\operatorname {arccot} {239}}
恒等式
下面恒等式均适用于函数2(取最小同界角的反余切函数) [函数 2]
arccot
x
=
π
2
−
arctan
x
{\displaystyle \operatorname {arccot} x={\frac {\pi }{2}}-\arctan x}
arccot
(
−
x
)
=
π
−
arccot
x
{\displaystyle \operatorname {arccot}(-x)=\pi -\operatorname {arccot} x\!}
arccot
1
x
=
π
2
−
arccot
x
=
arctan
x
,
{\displaystyle \operatorname {arccot} {\frac {1}{x}}={\frac {\pi }{2}}-\operatorname {arccot} x=\arctan x,\ }
x
>
0
{\displaystyle \ x>0}
arccot
1
x
=
3
π
2
−
arccot
x
=
π
+
arctan
x
,
{\displaystyle \operatorname {arccot} {\frac {1}{x}}={\frac {3\pi }{2}}-\operatorname {arccot} x=\pi +\arctan x,\ }
x
<
0
{\displaystyle \ x<0}
和差
arccot
x
+
arccot
y
=
arccot
x
y
−
1
x
+
y
,
x
>
−
y
{\displaystyle \operatorname {arccot} x+\operatorname {arccot} y=\operatorname {arccot} {\frac {xy-1}{x+y}},x>-y}
arccot
x
+
arccot
y
=
arccot
x
y
−
1
x
+
y
+
π
,
x
<
−
y
{\displaystyle \operatorname {arccot} x+\operatorname {arccot} y=\operatorname {arccot} {\frac {xy-1}{x+y}}+\pi ,x<-y}
arctan
x
+
arccot
x
=
π
2
{\displaystyle \arctan x+\operatorname {arccot} x={\frac {\pi }{2}}}
积分
∫
arccot
x
c
d
x
=
x
arccot
x
c
+
c
2
ln
(
c
2
+
x
2
)
{\displaystyle \int \operatorname {arccot} {\frac {x}{c}}\ dx=x\operatorname {arccot} {\frac {x}{c}}+{\frac {c}{2}}\ln(c^{2}+x^{2})}
∫
x
arccot
x
c
d
x
=
c
2
+
x
2
2
arccot
x
c
+
c
x
2
{\displaystyle \int x\operatorname {arccot} {\frac {x}{c}}\ dx={\frac {c^{2}+x^{2}}{2}}\operatorname {arccot} {\frac {x}{c}}+{\frac {cx}{2}}}
∫
x
2
arccot
x
c
d
x
=
x
3
3
arccot
x
c
+
c
x
2
6
−
c
3
6
ln
(
c
2
+
x
2
)
{\displaystyle \int x^{2}\operatorname {arccot} {\frac {x}{c}}\ dx={\frac {x^{3}}{3}}\operatorname {arccot} {\frac {x}{c}}+{\frac {cx^{2}}{6}}-{\frac {c^{3}}{6}}\ln(c^{2}+x^{2})}
∫
x
n
arccot
x
c
d
x
=
x
n
+
1
n
+
1
arccot
x
c
+
c
n
+
1
∫
x
n
+
1
c
2
+
x
2
d
x
,
n
≠
1
{\displaystyle \int x^{n}\operatorname {arccot} {\frac {x}{c}}\ dx={\frac {x^{n+1}}{n+1}}\operatorname {arccot} {\frac {x}{c}}+{\frac {c}{n+1}}\int {\frac {x^{n+1}}{c^{2}+x^{2}}}\ dx,\quad n\neq 1}
参见 注释 参考文献
^ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 Zwillinger, D. (Ed.). "Inverse Circular Functions." §6.3 in CRC Standard Mathematical Tables and Formulae (页面存档备份 ,存于互联网档案馆 ). Boca Raton, FL: CRC Press, pp. 465-467, 1995.
^ 2.0 2.1 2.2 2.3 Weisstein, Eric W. "Inverse Cotangent (页面存档备份 ,存于互联网档案馆 )." From MathWorld--A Wolfram Web Resource.
^ 反餘切arccotangent反余切-学术名词资讯 Archive.is 的存档 ,存档日期2014-08-08 国家教育研究院 terms.naer.edu.tw [2014-08-07]^ 4.0 4.1 4.2 4.3 Abramowitz, M. and Stegun, I. A. (Eds.). "Inverse Circular Functions." §4.4 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing (页面存档备份 ,存于互联网档案馆 ). New York: Dover, pp. 79-83, 1972.
^ 5.0 5.1 Harris, J. W. and Stocker, H. Handbook of Mathematics and Computational Science (页面存档备份 ,存于互联网档案馆 ). New York: Springer-Verlag, p. 311, 1998.
^ 6.0 6.1 Jeffrey, A. "Inverse Trigonometric and Hyperbolic Functions." §2.7 in Handbook of Mathematical Formulas and Integrals, 2nd ed . Orlando, FL: Academic Press, pp. 124-128, 2000.
^ Т. Л. Корнієнко,В. І. Фіготіна. Алгебра і початки аналізу. 10 клас. Академічний рівень: Розробки уроків . Ranok Publishing House Ltd. : 205. ISBN 9786115403899 (乌克兰文 ) ^ ACOT 函数 (页面存档备份 ,存于互联网档案馆 ) office.microsoft.com [2014-08-07]^ Gradshtein, I. S., I. M. Ryzhik, et al. (2000). Table of integrals, series, and products, Academic Pr.
^ Lehmer, Derrick Henry. "On arccotangent relations for π." American Mathematical Monthly (1938): 657-664.
^ Raymond A. Barnett, Michael R. Ziegler, Karl E. Byleen. Analytic Trigonometry with Applications . John Wiley & Sons. 2011: 307. ISBN 9780470648056 ^ 周忠荣. 1.2.5.4 反餘切函數. 应用数学 . 清华大学出版社有限公司. 2005: 13 [2020-10-03 ] . ISBN 9787302112167存档 于2019-05-16). ^ Denise Szecsei. Trigonometry . Career Press. 2005: 87. ISBN 9781564149138 ^ arccot (页面存档备份 ,存于互联网档案馆 ) itl.nist.gov [2014-08-07]^ Domain of Arccot (页面存档备份 ,存于互联网档案馆 ) mathforum.org [2014-08-07]^ 《 Exponentielle & logarithme 》, § Fonctions circulaires réciproques, Dictionnaire de mathématiques – algèbre, analyse, géométrie , Encyclopædia Universalis.
^ Sloane, N. J. A. Sequences (OEIS 数列A005408 )/M2400 and (OEIS 数列A091007 ) in "The On-Line Encyclopedia of Integer Sequences."
^ Wetherfield, M. "The Enhancement of Machin's Formula by Todd's Process." Math. Gaz. 80, 333-344, 1996.
^ Wrench Jr, J. W., and L. B. Smith. "Values of the terms of the Gregory series for arccot 5 and arccot 239 to 1150 and 1120 decimal places, respectively." Mathematical Tables and other Aids to Computation 4 (1950): 160-161.
Bennett, A. A. "The Four Term Diophantine Arccotangent Relation." Ann. Math. 27, 21-24, 1926.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed (页面存档备份 ,存于互联网档案馆 ). Boca Raton, FL: CRC Press, pp. 142-143, 1987.
Bronshtein, I. N. and Semendyayev, K. A. Handbook of Mathematics, 3rd ed (页面存档备份 ,存于互联网档案馆 ). New York: Springer-Verlag, p. 70, 1997.
Castellanos, D. "The Ubiquitous Pi. Part I." Math. Mag. 61, 67-98, 1988a.
Valentine, Willard L. "A study of learning curves: II. The relationship between the hyperbola and the arc cotangent function." The Journal of General Psychology 4.1-4 (1930): 359-362.
Valentine, WILLARD L. "A study of learning curves. I. The application of Meyer's arc cotangent function and Thurstone's hyperbola to the maze performance of white rats." Journal of Comparative Psychology 10.4 (1930): 421.
Castellanos, D. "The Ubiquitous Pi. Part II." Math. Mag. 61, 148-163, 1988b.
Lehmer, D. H. "A Cotangent Analogue of Continued Fractions." Duke Math. J. 4, 323-340, 1938a.
Valentine, Willard L. "A study of learning curves: III. The relationship between a growth curve and the arc cotangent function." The Journal of General Psychology 5.2 (1931): 251-255.
Lehmer, D. H. "On Arccotangent Relations for pi." Amer. Math. Monthly 45, 657-664, 1938b.
Spanier, J. and Oldham, K. B. "Inverse Trigonometric Functions." Ch. 35 in An Atlas of Functions (页面存档备份 ,存于互联网档案馆 ). Washington, DC: Hemisphere, pp. 331-341, 1987.
Bennett, A. A. "The four term Diophantine arccotangent relation." Annals of Mathematics (1925): 21-24.
外部链接 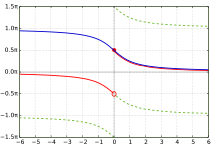
![[0,\pi ]](/media/math_img/2105/3e2a912eda6ef1afe46a81b518fe9da64a832751.svg)
![{\displaystyle [0,180^{\circ }]}](/media/math_img/2105/d1a22dc4758c76bc17559be79e50eec36b292c33.svg)
![{\displaystyle (-{\frac {\pi }{2}},{\frac {\pi }{2}}]}](/media/math_img/2105/a91a44d576e5cafae20687acc5b488948b4f6143.svg)
![{\displaystyle (-90^{\circ },90^{\circ }]}](/media/math_img/2105/14f9812826a015ccca5d98ad77828227b2c1304c.svg)